Descriptive Statistics

What is descriptive statistics?

  • summarize a given data set
  • measures of:
    • distribution (how data is spread out and how frequently different values occur)
    • central tendency (mean, median, mode)
    • variability (range, standard deviation, variance, interquartile range – IQR)

The data

We will be using US demographic data for our exploratory analyses.

You can download the csv file and add it to your RStudio (or Posit Cloud) project.

Create a new R script file and save it as county-data-analysis.R and load the tidyverse package and the data.

library(tidyverse)
county <- read_csv("data/county.csv")

Review of steps

Let’s practice what we have covered so far, which is the following:

  1. Summarize the data by calculating the mean of the numeric variables
  2. Create a scatter plot of two numeric variables
county |>
  summarize(mean_poverty = mean(poverty, na.rm = TRUE))

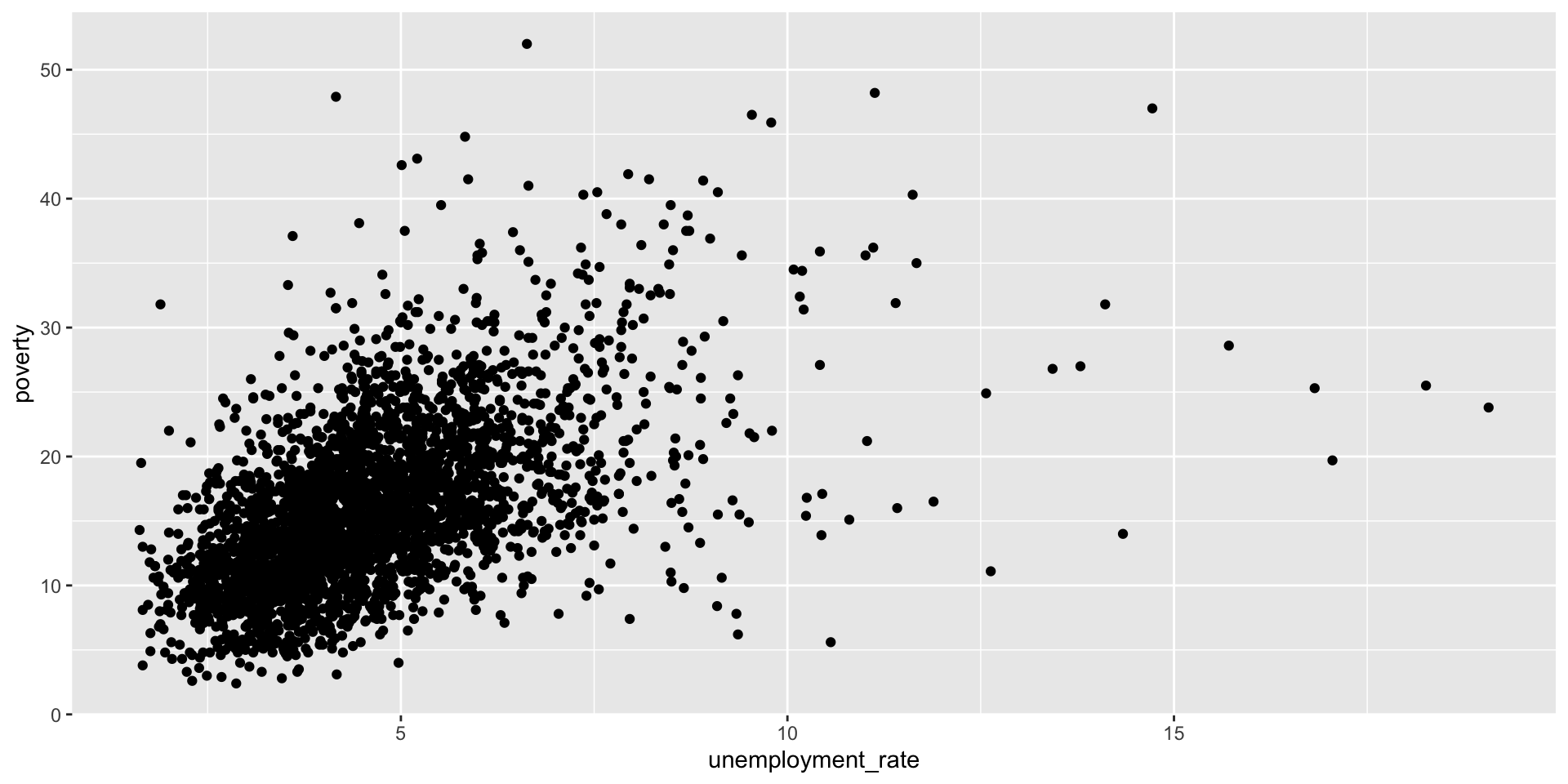
Scatterplot

county |>
  ggplot(aes(y = poverty, x = unemployment_rate)) +
  geom_point()

Distribution

How data is spread out and how frequently different values occur.

Histogram: the frequency distribution of a continuous variable

county |>
  ggplot(aes(x = unemployment_rate)) + 
  geom_histogram()

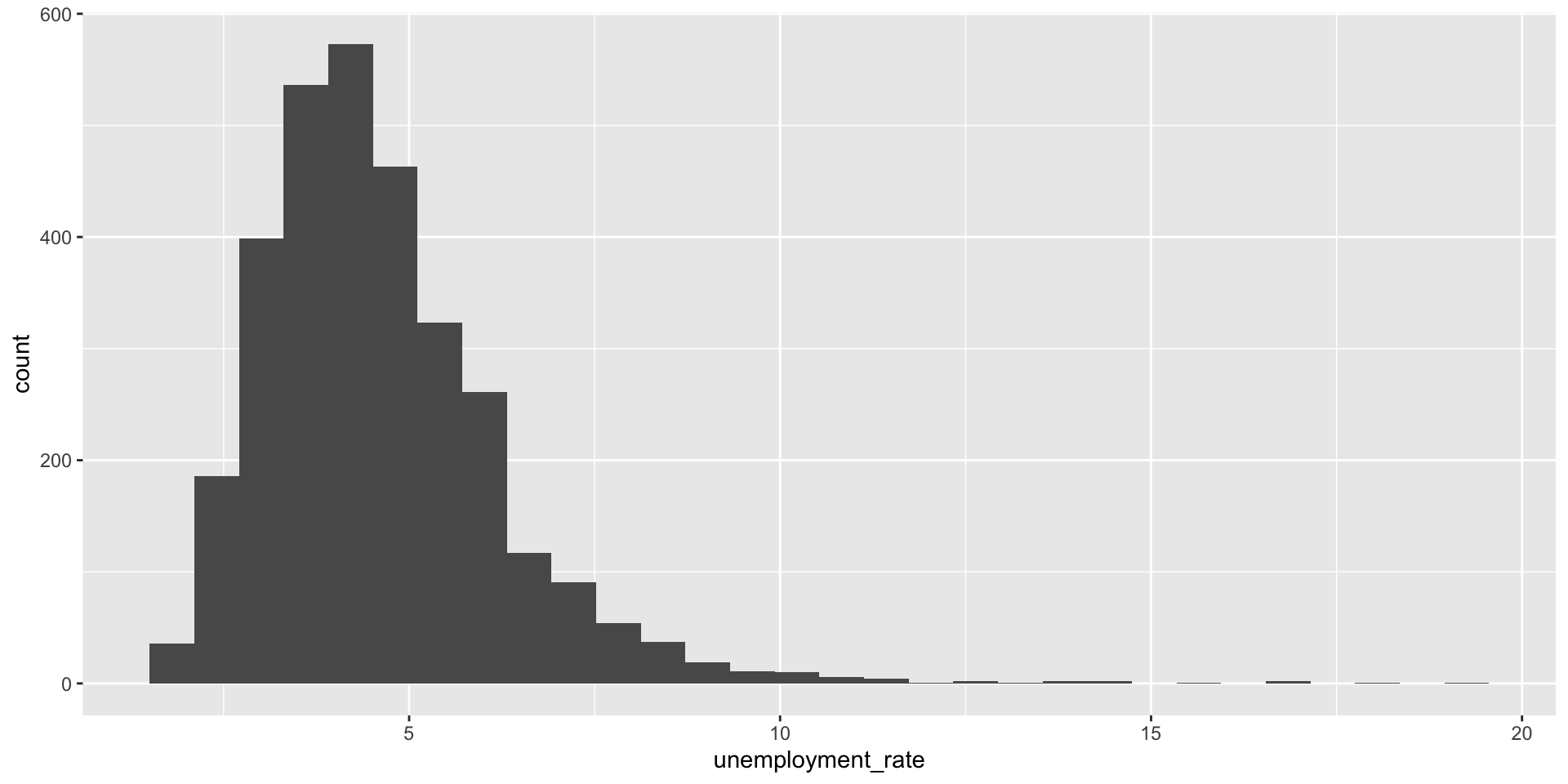
Histogram

  • Provides a view of the data density
  • Describes the sahpe of the data distribution
  • Higher bars represent where what values are more common

Histogram

  • x-axis shows the data ranges (bins)
  • y-axis shows the frequency (count or percentage)
  • bins: intervals the data range is divided into, each bin displays one bar
  • the height of each bar shows how many data points fall within that bin
  • the shape shows the distribution pattern (normal, skewed, bimodal, etc.)
  • the width of the bins can be manipulated

Histogram

The defaul number of bins for geom_histogram() is 30, but we can change that.

county |>
  ggplot(aes(x = unemployment_rate)) + 
  geom_histogram(bins = 100)

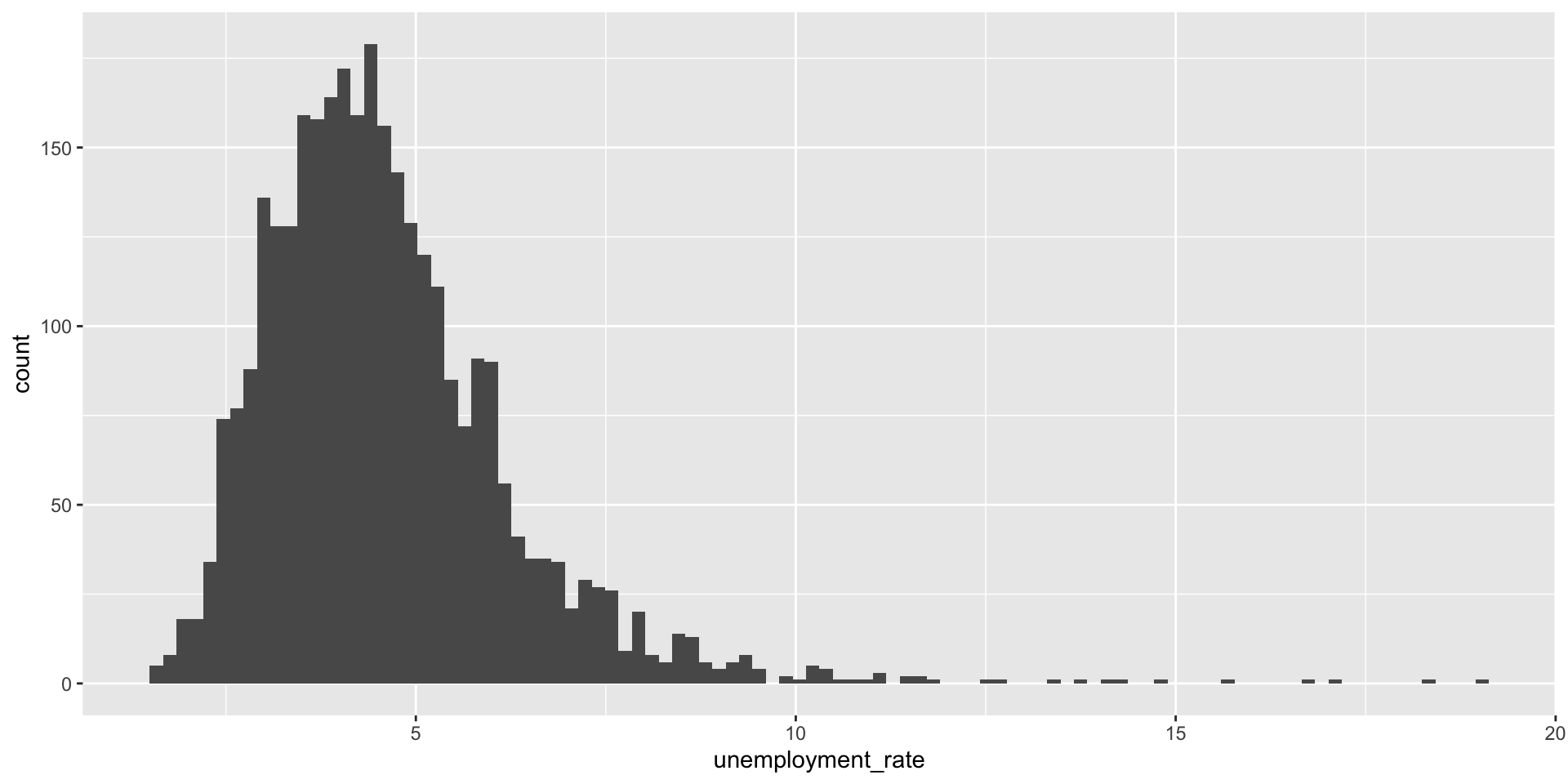
This distribution is skewed to the right, with a long tail to the right

Positive Skew

Or right-skewed

  • Most values cluster on the left
  • Some high values pull the mean up
  • The mean is greater than the median
county |>
  summarize(mean_unemployment = mean(unemployment_rate, na.rm = TRUE),
            median_unemployment = median(unemployment_rate, na.rm = TRUE))

Mean

The mean is the sum of the terms divided by the number of terms.

Here’s the formula for the sample (the observations) mean:

\(\bar{x} = \frac{x_1 + x_2 ... + x_n}{n}\)

where \(x_1, x_2, ..., x_n\) represent the observed values

Or:

\(\bar{x } = \frac{ \sum_{i=1}^n x_i}{n}\)

Median

The sample median is the middle value when data is arranged in order from lowest to highest.

For odd n:

  1. Order the data from smallest to largest
  2. Median = value in position \((n+1)/2\)

For even n:

  1. Order the data from smallest to largest
  2. Median = average of values in positions \(n/2\) and \((n/2)+1\)

Measures of Central Tendency

  • Mean
  • Median
  • Mode

Mode

  • value(s) that appears most frequently in the data

It’s the only measure of central tendency that can be used with categorical data.

A dataset can have:

  • One mode (unimodal)
  • Two modes (bimodal)
  • More than two modes (multimodal)
  • No mode (if all values occur exactly once)

Measures of Central Tendency

county |>
  count(unemployment_rate, sort = TRUE)

Variability – range

  • simplest measure of variability
  • the difference between the largest and smallest values
  • sensitive to outliers (uses two values)
  • nothing about how values are distributed between the min and max
county |>
  summarize(min_unemployment = min(unemployment_rate, na.rm = TRUE),
            max_unemployment = max(unemployment_rate, na.rm = TRUE)) |>
  mutate(range_unemployment = max_unemployment - min_unemployment)

Variability – variance

  • average squared distances from observations to the mean

\(s^2 = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}\)

Why do we use the squared deviation in the calculation of variance?

  • To get rid of negative values so that observations equally distant from the mean are weighed equally
  • To weigh larger deviations more heavily

Variability – standard deviation

  • square root of the variance
  • interpreted as the average distance of each data point from sample mean
  • the degree of dispersion of the data points relative to its mean

\(s = \sqrt{s^2}\)

Or:

\(s = \sqrt{ \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}}\)

Variability – standard deviation

  • square root of the variance
  • interpreted as the average distance of each data point from sample mean
  • the degree of dispersion of the data points relative to its mean
county |>
  summarize(sd_unemployment = sd(unemployment_rate, na.rm = TRUE))

Interquartile Range – IQR

  • quartiles are the partitioned values that divide the values into 4 equal parts (3 quartiles)
  • IQR is difference between the third and the first quartile So, there are
  • the first quartile (or 25th percentile) is denoted by \(Q1\) and known as the lower quartile
  • the second quartile (or 50th percentile) is denoted by \(Q2\) and known as the median
  • the third quartile (or 75th percentile) is denoted by \(Q3\) and known as the upper quartile

Interquartile Range – IQR

  • the interquartile range is equal to the upper quartile minus lower quartile
  • between \(Q1\) and \(Q2\) is the middle 50% of the data

\(IQR = Q3 - Q1\)

Box plot

  • the box represents the middle 50% of the data
  • the thick line in the middle is the median
  • top box line is \(Q3\)
  • bottom box line is \(Q1\)
  • whiskers:
    • max upper whisker reach = \(Q3 + 1.5 * IQR\)
    • max upper whisker reach = \(Q1 - 1.5 * IQR\)

Box plot

county |>
  ggplot(aes(y = unemployment_rate)) +
  geom_boxplot()

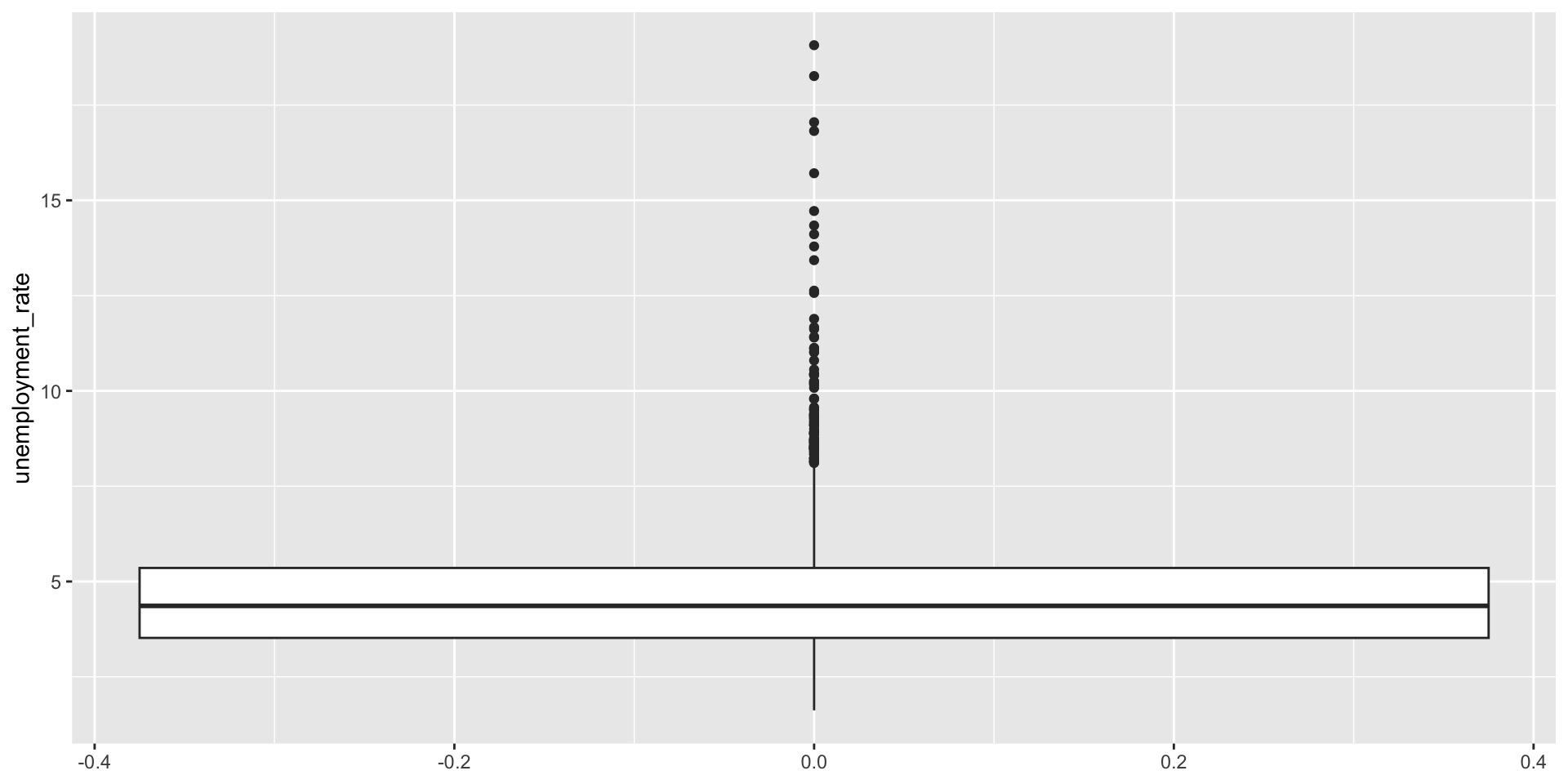
Outliers

  • potential outliers are shown in the box plot as dots
  • an outlier is an observation that:
    • is beyond the maximun reach of the whiskers
    • appears extreme, relative to the rest of the data