Graphs
CSCI 1913 – Introduction to Algorithms, Data Structures, and Program Development
Adriana Picoral
Adriana Picoral
Graph
- A graph contains nodes and edges (like a tree)
- unlike a tree, a graph can have loops
- we call graph “nodes” vertices – A, B, C, D and E are vertices
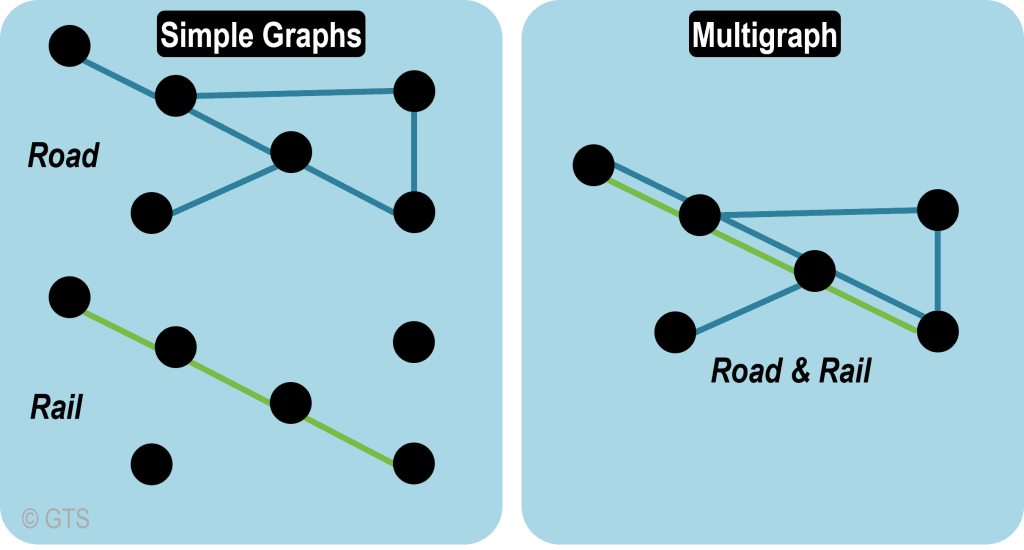
Simple and multigraphs
- Simple graphs have their nodes connected by only one link/edge
Simple and multigraphs
- Simple graphs have their nodes connected by only one link/edge
- Multigraphs can have multiple types of links/edges between nodes/vertices
Simple and multigraphs
- Simple graphs have their nodes connected by only one link/edge
- Multigraphs can have multiple types of links/edges between nodes/vertices
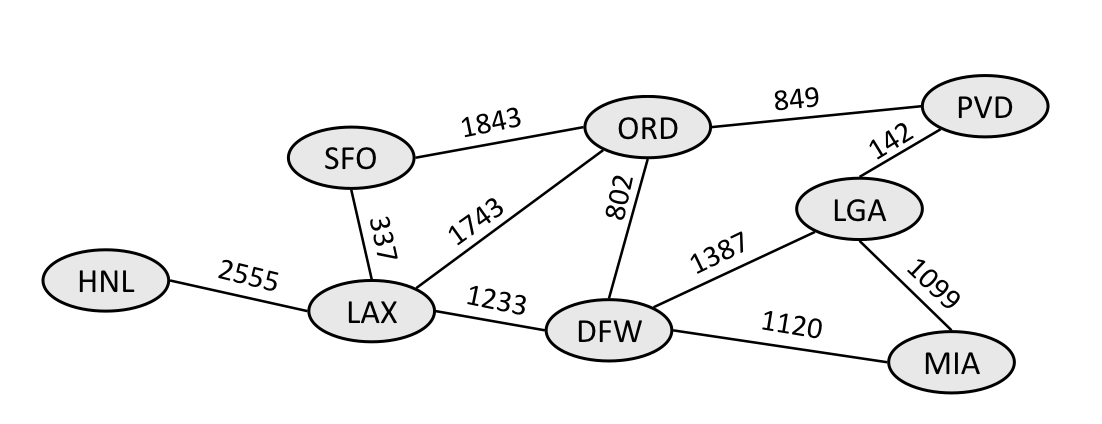
Weighted Graph
- A graph is considered weighted if it has numbers associated with edges. Weighted graphs are particularly useful for applications such as mapping between two locations, to take into consideration traffic, distance, time, etc.
- Here is an example weighted graph of airline flights, with the weights representing the miles between airports
Direct vs. Undirected
- if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person A can shake hands with a person B only if B also shakes hands with A.
- if an edge from a person A to a person B means that A owes money to B, then this graph is directed, because owing money is not necessarily reciprocated.
Undirected Graph
Any person can shake hands with another person only if that other person also shakes hands with the first person.
Direct Graph
if an edge from a person A to a person B means that A owes money to B, then this graph is directed, because owing money is not necessarily reciprocated.
How can we represent a graph?
Graph Representation
- Adjacency Matrix
- Adjacency List
- Edge List
Adjacency Matrix
0 0 0 0 0 0 0
0 1 1 0 0 1 0
0 1 0 1 0 1 0
0 0 1 0 1 0 0
0 0 0 1 0 1 1
0 1 1 0 1 0 0
0 0 0 0 1 0 0Adjacency Matrix
You can use an adjacency Matrix for direct graphs, indicating that either
- There is an edge from i to j
- There is an edge from j to i
Adjacency List
An adjacency list is a graph representation where each for each vertex you store a list of neighbouring verticies.
0 -> {}
1 -> {1, 2, 5}
2 -> {1, 5, 3}
3 -> {2, 4,}
4 -> {3, 5, 6}
5 -> {1, 2, 4}
6 -> {4}There are different ways to do this implementation: with hash tables, arrays, lists, with OOP and vertex and edge classes.
Adjacency List
0 -> {}
1 -> {1, 2, 5}
2 -> {1, 5, 3}
3 -> {2, 4}
4 -> {3, 5, 6}
5 -> {1, 2, 4}
6 -> {4}Adjacency List
0 -> {2, 1}
1 -> {3, 4}
2 -> {3}
3 -> {4}
4 -> {}Adjacency Matrix vs Adjacency List
- Adjacency Lists are more space efficient that Adjacency Matrix
- Different operations have different costs
- In an adjacency list neighbors of each vertex are listed efficiently compared to the “degree” of the vertex
- In adjacency matrix checking if two nodes are connected is constant time
- Linear Systems of equations are easier with adjacency Matrix
Edge List
We can also represent a graph by storing a list of edges.
[[0, 1], [0, 2], [0,3], [1,3], [1,4], [2,3], [3, 4]]